Likelihood profile for various measurement error values

Estimates the standard deviation of measurement error (sign) of the response variable, an input of the cbvn() function, when a measured value is not available (Lark & Milne, 2016). sigh is fixed at each of a set of values in turn, and remaining parameters are estimated conditional on sigh by maximum likelihood. The maximized likelihoods for the sequence of values constitutes a likelihood profile. The value of sigh where the profile is maximized is selected.

Usage

ble_profile(data, sigh, model="lp", equation=NULL,  start, UpLo="U",
             optim.method="BFGS", plot=TRUE)

Arguments

data

A dataframe with two numeric columns, independent (x) and dependent (y) variables respectively.

sigh

A vector of the suggested standard deviations of the measurement error values.

model

Selects the functional form of the boundary line. It includes "blm" for linear model, "lp" for linear plateau model, "mit" for the Mitscherlich model, "schmidt" for the Schmidt model, "logistic" for logistic model, "logisticND" for logistic model proposed by Nelder (1961), "inv-logistic" for the inverse logistic model, "double-logistic" for the double logistic model, "qd" for quadratic model and the "trapezium" for the trapezium model. For custom models, set model = "other".

equation

A custom model function writen in the form of an R function. Applies only when argument model="other", else it is NULL.

start

A numeric vector of initial starting values for optimization in fitting the boundary model. Its length and arrangement depend on the suggested model:

For the "blm" model, it is a vector of length 7 arranged as the intercept, the slope, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "lp" model, it is a vector of length 8 arranged as the intercept, the slope, the maximum or plateau response, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "mit" model, it is a vector of length 8 arranged as the intercept, shape parameter, the maximum or plateau response, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "logistic", "inv-logistic" and "logisticND" models, it is a vector of length 8 arranged as scaling parameter, shape parameter, the maximum or plateau value, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "double-logistic" model, it is a vector of length 11 arranged as scaling parameter, shape parameter, maximum response, maximum response, scaling parameter two, shape parameter two, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "trapezium" model, it is a vector of length 10 arranged as intercept one, slope one, maximum response, intercept two, slope two, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "qd" model, it is a vector of length 8 arranged as a constant, linear coefficient, quadratic coefficient,mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.
For the "schmidt" model, it is a vector of length 8 arranged the scaling parameter, shape parameter (x-value at maximum response ), maximum response, mean of x, mean of y, standard deviation of x, standard deviation of y and the correlation of x and y.

UpLo

Selects the type of boundary. "U" fits the upper boundary and "L" fits the lower boundary.

optim.method

Describes the method used to optimize the model as in the optim() function. The methods include "Nelder-Mead", "BFGS", "CG", "L-BFGS-B", "SANN" and "Brent".

plot

If TRUE, a plot is part of the output. If FALSE, plot is not part of output (default is TRUE).

Value

A list of length 2 containing the suggested standard deviations of measurement error values and the corresponding log-likelihood values. additionally, a likelihood profile plot (log-likelihood against the standard deviation of measurement error) is produced.

Details

Some inbuilt models are available for the cbvn() function. The suggest model forms are as follows:

Linear model ("blm") $$y=\beta_1 + \beta_2x$$ where $\beta_1$ is the intercept and $\beta_2$ is the slope.
Linear plateau model ("lp") $$y= {\rm min}(\beta_1+\beta_2x, \beta_0)$$ where $\beta_1$ is the intercept , $\beta_2$ is the slope and $\beta_0$ is the maximum response.
The logistic ("logistic") and inverse logistic ("inv-logistic") models $$ y= \frac{\beta_0}{1+e^{\beta_2(\beta_1-x)}}$$ $$ y= \beta_0 - \frac{\beta_0}{1+e^{\beta_2(\beta_1-x)}}$$ where $\beta_1$ is a scaling parameter , $\beta_2$ is a shape parameter and $\beta_0$ is the maximum response.
Logistic model ("logisticND") (Nelder (1961)) $$ y= \frac{\beta_0}{1+(\beta_1 \times e^{-\beta_2x})}$$ where $\beta_1$ is a scaling parameter, $\beta_2$ is a shape parameter and $\beta_0$ is the maximum response.
Double logistic model ("double-logistic") $$ y= \frac{\beta_{0,1}}{1+e^{\beta_2(\beta_1-x)}} - \frac{\beta_{0,2}}{1+e^{\beta_4(\beta_3-x)}}$$ where $\beta_1$ is a scaling parameter one, $\beta_2$ is shape parameter one, $\beta_{0,1}$ and $\beta_{0,2}$ are the maximum response , $\beta_3$ is a scaling parameter two and $\beta_4$ is a shape parameter two.
Quadratic model ("qd") $$y=\beta_1 + \beta_2x + \beta_3x^2$$ where $\beta_1$ is a constant, $\beta_2$ is a linear coefficient and $\beta_3$ is the quadratic coefficient.
Trapezium model ("trapezium") $$y={\rm min}(\beta_1+\beta_2x, \beta_0, \beta_3 + \beta_4x)$$ where $\beta_1$ is the intercept one, $\beta_2$ is the slope one, $\beta_0$ is the maximum response, $\beta_3$ is the intercept two and $\beta_3$ is the slope two.
Mitscherlich model ("mit") $$y= \beta_0 - \beta_1*\beta_2^x$$ where $\beta_1$ is the intercept, $\beta_2$ is a shape parameter and $\beta_0$ is the maximum response.
Schmidt model ("schmidt") $$y= \beta_0 + \beta_1(x-\beta_2)^2$$ where $\beta_1$ is ascaling parameter, $\beta_2$ is a shape parameter (x-value at maximum response ) and $\beta_0$ is the maximum response .

The function ble_profile() utilities the optimization procedure of the optim() function to determine the model parameters. There is a tendency for optimization algorithms to settle at a local optimum. To remove the risk of settling for local optimum parameters, it is advised that the function is run using several starting values and the results with the largest likelihood can be taken as a representation of the global optimum.

The common errors encountered due to poor start values

function cannot be evaluated at initial parameters
initial value in 'vmmin' is not finite

References

Lark, R. M., & Milne, A. E. (2016). Boundary line analysis of the effect of water filled pore space on nitrous oxide emission from cores of arable soil. European Journal of Soil Science, 67 , 148-159.

Nelder, J.A. 1961. The fitting of a generalization of the logistic curve. Biometrics 17: 89–110.

Author

Chawezi Miti <chawezi.miti@nottingham.ac.uk>

Examples


x<-evapotranspiration$`ET(mm)`
y<-evapotranspiration$`yield(t/ha)`
data<-data.frame(x,y)
start<-c(0.5,0.02,289.6,2.4,83.7,1.07,0.287)
sigh <- c(0.6,0.7,0.8,0.9)

ble_profile(data,start=start,model = "blm", sigh = sigh)

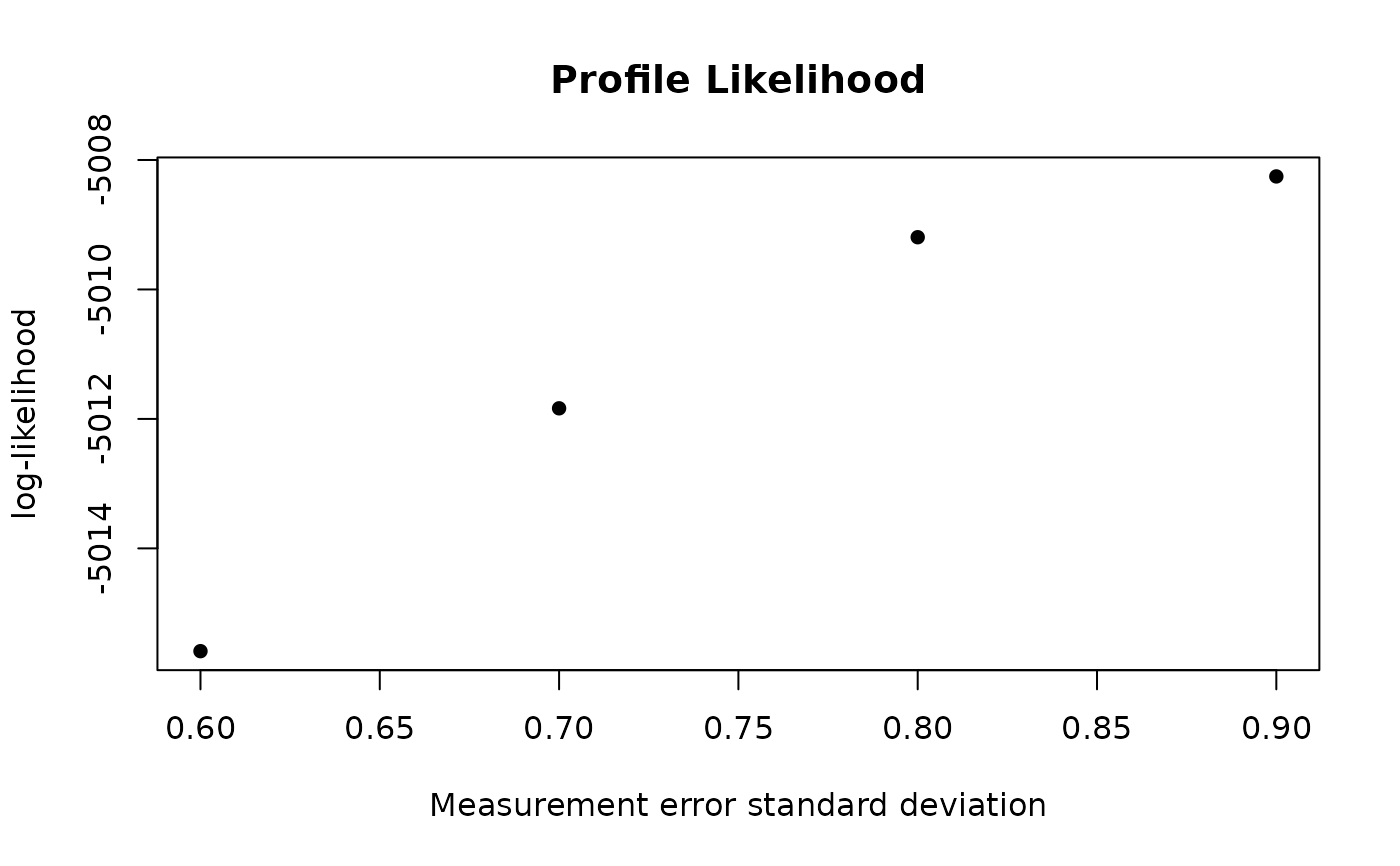#> $`log-likelihood`
#> [1] -5015.588 -5011.836 -5009.193 -5008.254
#> 
#> $Merror
#> [1] 0.6 0.7 0.8 0.9
#>